|
|
|
Главная – Журналы – Сибирский журнал вычислительной математики 2025 номер 3
2025 год, номер 3
|
А.Л. Агеев, Т.В. Антонова
Институт математики и механики им. Н.Н. Красовского Уральского отделения Российской академии наук, Екатеринбург, Россия
ageev@imm.uran.ru
Ключевые слова: некорректная задача, метод регуляризации, линии разрыва, глобальная локализация, дискретизация, порог разделимости, сепарация изображений
Страницы: 241-256
Аннотация >>
Рассматривается некорректно поставленная задача локализации (определения положения) линий разрыва функции двух переменных при условии, что вне линий разрыва функция удовлетворяет условию Липшица, а в каждой точке на линии имеет разрыв первого рода. Для равномерной сетки с шагом τ предполагается, что в каждом узле известны средние значения на квадрате со стороной τ от возмущенной функции, и возмущенная функция приближает точную функцию в пространстве L2(R2). Уровень возмущения δ считается известным. Предлагается новый подход к построению регуляризирующих алгоритмов локализации линий разрыва на основе сепарации исходных зашумленных данных. На классе функций с кусочно-линейными линиями разрыва построены новые алгоритмы и доказана теорема сходимости с оценками точности аппроксимации.
DOI: 10.15372/SJNM20250301
EDN: LVLVPW
|
|
Н.А. Артемова1, О.В. Ушакова1,2
1Институт математики и механики им. Н.Н. Красовского Уральского отделения Российской академии наук, Екатеринбург, Россия
ana@imm.uran.ru
2Уральский федеральный университет им. первого Президента России Б.Н. Ельцина, Екатеринбург, Россия
uov@imm.uran.ru
Ключевые слова: структурированные сетки, деформированные объемы, оптимальные сетки, подвижные сетки
Страницы: 257-267
Аннотация >>
Описывается алгоритм морфинга, пополнивший технологию построения трехмерных структурированных сеток, предназначенную для численного решения дифференциальных уравнений, моделирующих вихревые процессы многокомпонентной гидродинамики. Алгоритм морфинга предназначен для построения структурированных сеток особой структуры в объемах, полученных деформацией объемов вращения телами, образованными поверхностями вращения с параллельными осями. Алгоритм разработан в рамках вариационного подхода построения оптимальных сеток и является нестационарным: на каждой итерации меняется (деформируется) форма области и сетка для нее, затем сетка оптимизируется в соответствии с критериями оптимальности, т.е. близости сетки к равномерной и ортогональной. Итерации повторяются до тех пор, пока деформация объема не достигнет требуемой формы. Алгоритм позволяет строить сетки в областях очень сложной геометрии, при этом не нужно задавать границу области сложной формы, достаточно описать объем вращения, деформирующий объем и указать параметры деформации. Приводятся примеры расчетов сеток.
DOI: 10.15372/SJNM20250302
EDN: MRQLIH
|
|
Е.К. Гусева1,2, В.И. Голубев1, В.П. Епифанов2, И.Б. Петров1
1Московский физико-технический институт (национальный исследовательский университет), Долгопрудный, Россия
guseva.ek@phystech.su
2Институт проблем механики им. А.Ю. Ишлинского Российской академии наук, Москва, Россия
evp@ipmnet.ru
Ключевые слова: реология льда, упругопластичность, трещинообразование, гидростатическое ядро, нелинейные волны
Страницы: 269-286
Аннотация >>
В процессе приложения динамических нагрузок лёд демонстрирует сложное нелинейное поведение, зависящее от многих факторов, в том числе и от скорости деформирования. В прикладных задачах актуальными являются низкоскоростные столкновения, в которых лёд проявляет как вязкие, так и хрупкие свойства. Для отражения специфики локального разрушения льда в настоящей работе предлагается составная модель, выделяющая во льду гидростатическое ядро и упругопластическую зону, оставляя материал вдали от области удара упругим. Дополнительно учитывается объёмное трещинообразование. Верификация модели производится на основе сравнения результатов расчётов с лабораторным экспериментом со сферическим индентором. В результате численных расчётов удаётся воспроизвести явления, наблюдаемые в экспериментах. Реконструированы нелинейные волны, отражена волновая природа трещинообразования, получены характерные картины разрушения льда. Рассчитанные деформационные кривые подтверждают возможность качественного описания поведения льда на основной стадии удара.
DOI: 10.15372/SJNM20250303
EDN: NQWIZA
|
|
Х.Д. Икрамов
Московский государственный университет им. М.В. Ломоносова, Москва, Россия
ikramov@cs.msu.su
Ключевые слова: юнитоид, коквадрат, каноническая форма относительно конгруэнций, канонические углы, орбита конгруэнтности
Страницы: 287-292
Аннотация >>
Хорошо известно, что если диагонализуемые матрицы A и B коммутируют, то они могут быть приведены к диагональному виду одним и тем же преобразованием подобия. Мы устанавливаем аналог этого утверждения, относящийся к невырожденным юнитоидным матрицам и преобразованиям эрмитовой конгруэнции. Юнитоидными называются матрицы, приводимые к диагональному виду посредством конгруэнций.
DOI: 10.15372/SJNM20250304
EDN: NUYAJP
|
|
В. Крейнович1, С.П. Шарый2
1University of Texas at El Paso, El Paso, USA
vladik@utep.edu
2Федеральный исследовательский центр информационных и вычислительных технологий, Новосибирск, Россия
shary@ict.nsc.ru
Ключевые слова: интервал, полином, область значений, NP-трудная задача, полиномиально сложная задача, теорема Гаганова
Страницы: 293-303
Аннотация >>
Во многих практических ситуациях необходимо вычислять внешнюю оценку для области значений полинома от нескольких переменных f(x1,…,xn) на заданных интервалах [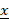 1, 1, 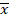 1],...,[ 1],...,[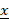 n, n, 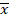 n] с определённой относительной погрешностью ε > 0. Известно, что эта задача является NP-трудной для всех ε < 1/8, но не было известно, является ли задача NP-трудной для других значений ε. В нашей статье даётся полный ответ на этот вопрос, а именно, мы доказываем, что рассматриваемая задача является NP-трудной для всех ε ≤ 1 и полиномиально разрешима для всех ε > 1. n] с определённой относительной погрешностью ε > 0. Известно, что эта задача является NP-трудной для всех ε < 1/8, но не было известно, является ли задача NP-трудной для других значений ε. В нашей статье даётся полный ответ на этот вопрос, а именно, мы доказываем, что рассматриваемая задача является NP-трудной для всех ε ≤ 1 и полиномиально разрешима для всех ε > 1.
DOI: 10.15372/SJNM20250305
EDN: OLQSLH
|
|
Н. Саха1, Дж. Шахни1, Р. Сингх1, В. Гулерия2, Н. Шривастав3
1Birla Institute of Technology Mesra, Ranchi, India
randhir.math@gmail.com
2National Institute of Advanced Manufacturing Technology Hatia, Ranchi, India
3Chandigarh University, Mohali, India
Ключевые слова: уравнение Эмдена-Фаулера, вейвлеты Лежандра, вейвлеты Хаара, единственность решения, интегральное уравнение, метод коллокации
Страницы: 305-326
Аннотация >>
Уравнения Эмдена-Фаулера широко используются в математическом и физическом моделировании. Они описывают явления в различных областях, включая астрофизику, квантовую механику и нелинейную динамику. Область их применения - от моделирования теплового поведения звезд до распределения компонентов химических реакций. Ученые постоянно ищут новые методы для более эффективного и точного решения уравнений Эмдена-Фаулера (ЭФ) ввиду их универсальности и разнообразия. В данной статье представлен новый подход к решению обобщенных уравнений ЭФ с учетом граничных условий с использованием вейвлетов Лежандра. Сначала мы преобразуем задачу в эквивалентные интегральные уравнения Фредгольма. Затем используем коллокационный подход вейвлетов Лежандра и итерационный метод Ньютона-Рафсона для решения получаемых в результате интегральных уравнений. Формулировка предлагаемого алгоритма дополняется анализом его сходимости и ошибок. Мы исследуем точность метода путем вычисления численного решения и ошибок с помощью различных примеров. Мы сравниваем наши численные результаты с точным решением и решениями, полученными с помощью методов, описанных в литературе, таких как метод вейвлетов Хаара и метод оптимального гомотопического анализа. С помощью коллокационного метода вейвлетов Лежандра может быть получена улучшенная точность при меньшем числе точек коллокации, что делает его использование более выгодным.
DOI: 10.15372/SJNM20250306
EDN: YRWRGF
|
|
М.Ю. Сахно
Омский филиал Федерального государственного бюджетного учреждения науки Института математики им. С.Л. Соболева Сибирского отделения Российской академии наук, Омск, Россия
sosnovskayamy@gmail.com
Ключевые слова: генетический алгоритм, оптимизированный кроссинговер, адаптивная схема, распараллеливаемые работы, энергия, расписание
Страницы: 327-346
Аннотация >>
В настоящей работе рассматриваются задачи составления расписаний с учетом расхода энергии. Такие задачи возникают в многопроцессорных компьютерных системах и учитывают ресурсные ограничения и возможности распараллеливания. Для этих задач известны алгоритмы жадного и списочного типов с гарантированными оценками точности в худшем случае. В настоящей работе предлагается адаптивный генетический алгоритм с декодировкой решений, основанной на специфике постановок рассматриваемых задач. Его особенностью является то, что в операторе кроссинговера решается задача оптимальной рекомбинации в полной и усеченной версиях. Вызов операторов кроссинговера реализуется адаптивно. Настройка категориальных и числовых параметров выполняется адаптивно современными пакетами. Результаты экспериментального исследования показали статистически значимое преимущество над известными алгоритмами на сериях задач различной структуры.
DOI: 10.15372/SJNM20250307
EDN: YXXQLD
|
|



